2023-01-03 19:02:48 乐山人事考试网 https://leshan.huatu.com/ 文章来源:乐山人事考试网
【导读】华图乐山人事考试网同步乐山人事考试网发布:2023年乐山市选调生考试报名时间,详细信息请阅读下文!如有疑问请加【乐山公招考试交流群汇总】 ,更多资讯请关注四川华图微信公众号(schuatu)。
2023年乐山市选调生考试报名时间
》》报名时间:2023年1月5日至1月11日上午8:00
》》报名网站:四川省人力资源和社会保障厅官网(http://rst.sc.gov.cn/)“人事考试”专栏。
》》确认缴费时间:2023年1月13日上午8:00前登陆报名网站确认缴费。
》》准考证打印:2月21日至2月25日
》》笔试时间:2月25日
| 原文公告 | 岗位表下载 |
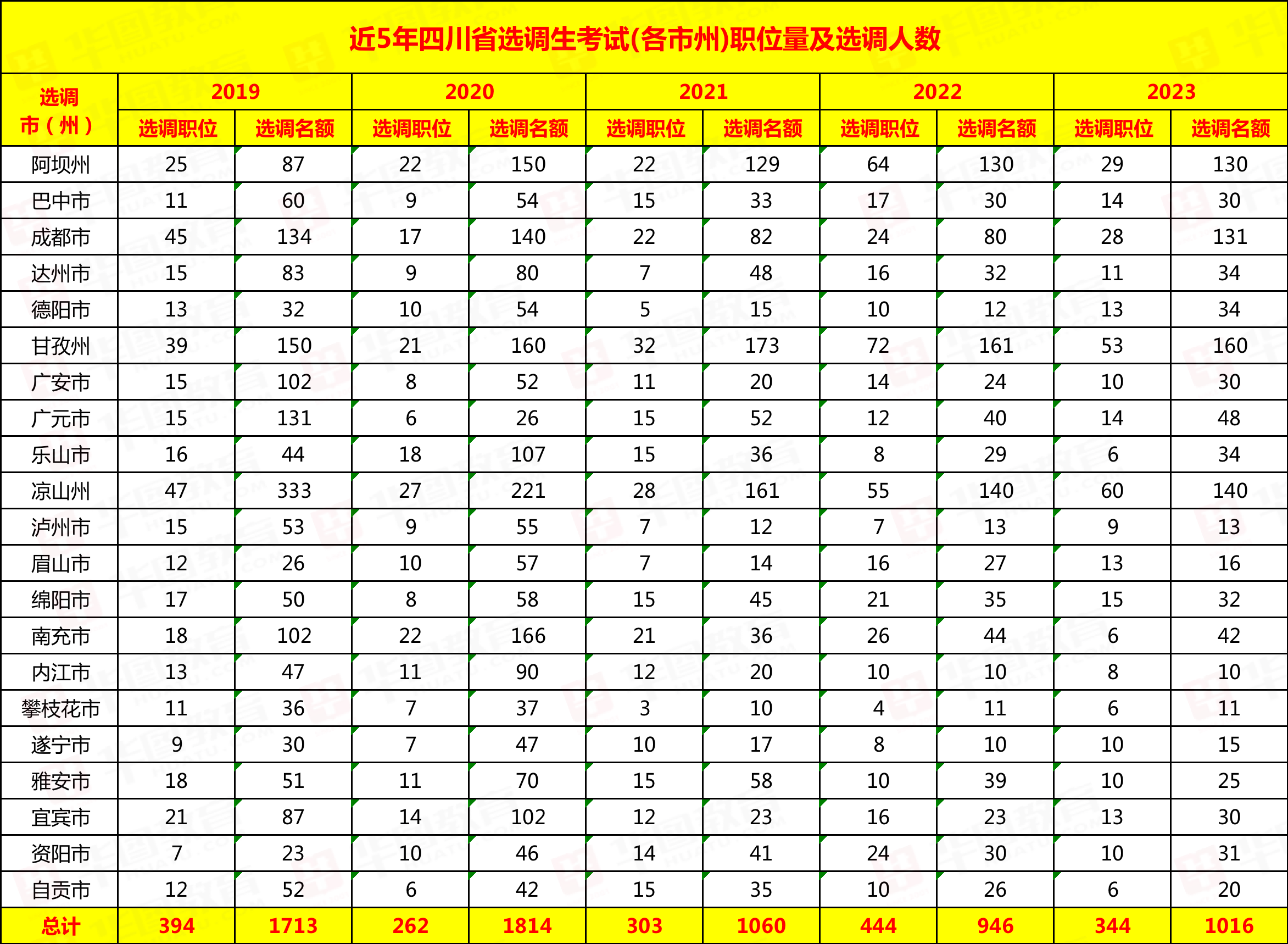
| 四川省2023年选调优秀大学毕业生到基层工作1016名公告 | 点击岗位表下载 |
》》2023乐山市选调生考试公告节选
(一)报名
本次选调采用网络方式报名。报名时间为2023年1月5日至1月11日上午8:00,报名网站为四川省人力资源和社会保障厅官网(http://rst.sc.gov.cn/)“人事考试”专栏。资格审查由各市(州)党委组织部负责,贯穿选调全过程。任何时候发现报考者有不符合选调资格条件、弄虚作假的情形,取消考试、录用资格,所产生的后果由报考者本人承担。报名及资格初审按以下程序进行:
1.网上报名。在选调范围内、符合选调条件的应届毕业生向所在院(系)党组织提出申请,院(系)党组织、高校(院所)党委组织部(或就业主管部门)按照选调范围、选调条件对毕业生政治素质、道德品行、资格条件、综合表现、专业特长、心理素质、遵纪守法等情况严格把关后,提出推荐意见。“服务基层项目人员”向服务地所在县(市、区)项目主管部门提出申请,经项目主管部门、县(市、区)党委组织部严格把关后,提出推荐意见。
在选调范围内、符合选调条件,且高校(院所)、县(市、区)有关部门同意推荐的人员,在报名时间内登陆报名网站,查阅“公告”“选调计划表”“报考指南”等,了解基本政策和要求,选择与自己条件相符的职位报名。报考者应使用第二代有效居民身份证有关信息进行报名,并且只能选择一个选调职位,其中“服务基层项目人员”须填报服务地所属市(州)职位。不得报考录用后即构成公务员法第七十四条所列情形的职位,也不得报考与本人有夫妻关系、直系血亲关系、三代以内旁系血亲关系以及近姻亲关系的人员担任领导成员的用人单位的职位。报名时填报的身份证信息必须与考试时使用的身份证一致。
2.填报信息。报考者按网络提示要求通过注册,如实、准确、完整填写《四川省2023年度选调优秀大学毕业生到基层工作报名推荐登记表》(以下简称《报名推荐表》)的各项内容(填写说明详见附件3《报考指南》),同时下载照片审核处理工具(在《报名推荐表》上传照片处下载)进行照片处理,并按网络提示上传照片。对伪造、变造有关证件、材料、信息,骗取考试资格的,按《公务员录用违规违纪行为处理办法》等有关规定处理。
3.查询资格初审结果。报考者请于2023年1月5日至1月12日上午8:00期间,登陆报名网站查询是否通过资格初审。资格初审合格者按网络提示打印《报名推荐表》两份,报院(系)党组织、高校(院所)党委组织部(或就业主管部门)等签署推荐意见并签章后,在面试资格审查时提交市(州)党委组织部。资格初审不合格的,可于报名时间截止前改报其他符合条件的职位。
》》2023乐山市选调生笔试资料
例题精析
【例 1】 某餐饮公司甲、 乙两种外卖每份的售价分别为 30 元和 50 元, 若该公司某天售出这两种外卖共 500 份, 销售收入为 21400 元, 则售出的两种外卖数量相差:
A. 140 份 B. 160 份
C. 180 份 D. 200 份
【答案】 A
【解析】 第一步, 本题考查基础应用题, 方程法解题。
第二步, 设甲卖了 x 份, 乙卖了 y 份, 根据一共卖 500 份和收入 21400 元, 可得方程 x+y = 500①; 30x+50y = 21400②; 解得 x = 180, y = 320, 所以差值为 140。
因此, 选择 A 选项。
【例 2】 植树节当天, 某学校的两个班自发组织了一些人去植树。 甲班每人植树 3 棵, 乙班每人植树 5 棵, 两个班共植树 115 棵。 那么, 两班植树人数之和最多为( ) 人 。
A. 36 B. 37
C. 38 D. 39
【答案】 B
【解析】 第一步, 本题考查不定方程问题。
第二步, 设甲班 x 人植树, 乙班 y 人植树, 根据题意列方程: 3x+5y = 115, 由倍数性质可知: 5y 是 5 的倍数, 115 也是 5 的倍数, 故 3x 也是 5 的倍数, 则 x 是 5 的倍数。第三步, 要使两班植树人数之和最多, 则 x 取值应最大, 因为 3×39 = 117 > 115, x
取值不超过 38, x 最大取 35, x = 35 时, 代入方程: 3×35+5y = 115, 解得: y = 2, 两班植树人数之和最多为 35+2 = 37 ( 人)。
因此, 选择 B 选项。
【例 3】 某学校组织一次教工接力比赛, 共准备了 25 件奖品分发给获得一、 二、 三
等奖的职工, 为设计获得各级奖励的人数, 制定两种方案: 若一等奖每人发 5 件, 二等奖每人发 3 件, 三等奖每人发 2 件, 刚好发完奖品; 若一等奖每人发 6 件, 二等奖每人发 3 件, 三等奖每人发 1 件, 也刚好发完奖品, 则获得二等奖的教工有多少人?
A. 6 B. 5
C. 4 D. 3
【答案】 A
【解析】 第一步, 本题考查不定方程问题, 用代入排除法解题。
第二步, 设一、 二、 三等奖的职工人数分别为 x、 y、 z, 根据共 25 件奖品, 两种方案都刚好发完, 列方程组: {5x+3y+2z = 25①, ②×2-①得: 7x+3y = 25。
第三步, 代入 A 选项, y = 6, 解得 x = 1, z = 1, 符合题意。因此, 选择 A 选项。
 扫码关注“乐山华图”
扫码关注“乐山华图”上一篇:2023年乐山市选调生笔试科目